一、楊輝三角形

　　1.1 楊輝三角形的概念

　　 楊輝三角，是二項式系數在三角形中的一種幾何排列。在歐洲，這個表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年發現這一規律的，比楊輝要遲393年，比賈憲遲600年。楊輝三角是中國古代數學的杰出研究成果之一，它把二項式系數圖形化，把組合數內在的一些代數性質直觀地從圖形中體現出來，是一種離散型的數與形的結合 。

        我們先看一下楊輝三角形的打印結果：

　　1.2 楊輝三角形的性質

　　 楊輝三角形有很多性質：

　　 1). 每行端點與結尾的數為1。

　　 2). 每個數等于它上方兩數之和。

　　 3). 每行數字左右對稱，由1開始逐漸變大。

　　 4). 第n行的數字有n項。

　　 5). 前n行共[(1+n)n]/2 個數。

　　 6).第n行的m個數可表示為 *C(n-1，m-1)*，即為從n-1個不同元素中取m-1個元素的組合數。

　　 7). 第n行的第m個數和第n-m+1個數相等 ，為組合數性質之一。

　　 8). 每個數字等于上一行的左右兩個數字之和。可用此性質寫出整個楊輝三角。即第n+1行的第i個數等于第n行的第i-1個數和第i個數之和，這也是組合數的性質之一。即 *C(n+1,i)=C(n,i)+C(n,i-1)*。

　　 9). (a+b)^n^的展開式中的各項系數依次對應楊輝三角的第(n+1)行中的每一項。

　　 10). 將第2n+1行第1個數，跟第2n+2行第3個數、第2n+3行第5個數……連成一線，這些數的和是第4n+1個斐波那契數;將第2n行第2個數(n>1)，跟第2n-1行第4個數、第2n-2行第6個數……這些數之和是第4n-2個斐波那契數。

　　 11). 將第n行的數字分別乘以10^(m-1)^，其中m為該數所在的列，再將各項相加的和為11^(n-1)^。 11^0^=1，

　　 11^1^=1 * 10^0^ + 1 * 10^1^=11，

　　 11^2^=1×10^0^+2x10^1^^+1x10^2^=121，

　　 11^3^=1x10^0^+3×10^1^+3x10^2^+1x10^3^=1331，

　　 11^4^=1x10^0^+4x10^1^10^2^+4x10^3+1x10^4=14641，

　　 11^5^=1x10^0^+5x10^1^+10x10^2^+10x10^3^+5x10^4^+1×10^5^=161051。

　　 12). 第n行數字的和為2^(n-1)^。1=2^(1-1)^，1+1=2^(2-1)^，1+2+1=2^(3-1)^，1+3+3+1=2^(4-1)^，1+4+6+4+1=2^(5-1)^，1+5+10+10+5+1=2^(6-1)^。

　　 13). 斜線上數字的和等于其向左(從左上方到右下方的斜線)或向右拐彎(從右上方到左下方的斜線)，拐角上的數字。1+1=2，1+1+1=3，1+1+1+1=4，1+2=3，1+2+3=6，1+2+3+4=10，1+3=4，1+3+6=10，1+4=5。

　　 14). 將各行數字左對齊，其右上到左下對角線數字的和等于斐波那契數列的數字。1，1，1+1=2，2+1=3，1+3+1=5，3+4+1=8，1+6+5+1=13，4+10+6+1=21，1+10+15+7+1=34，5+20+21+8+1=55。

　　實現楊輝三角形的打印也有很多方式，今天我為大家介紹兩種方式：

　　- 使用數組的方式：這也是網上比較常見的方式。需要使用數組，所以效率較低。

　　- 不使用數組的方式：不需要使用數組，所以效率較高。

　　二、使用數組的方式

　　2.1 示意圖

　　 根據上面的性質，如果我們要打印一個11行的楊輝三角形，我們可以將整個排列看做是一個n行，0-n列的矩陣，再結合上面的性質8，我們將這個矩陣用一個二維數組來實現，如下圖：

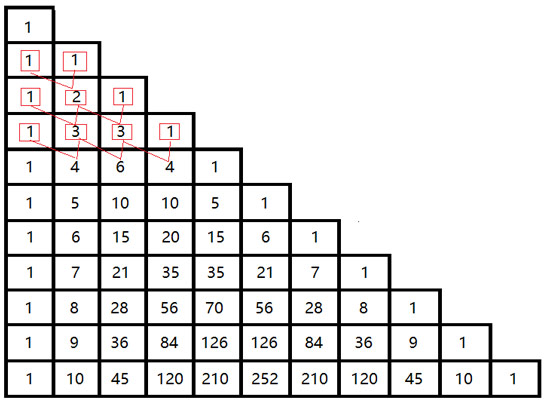
　　2.2 代碼分步實現

　　2.2.1 根據示意圖，我們先定義一個二維數組：

int n = 11;//要幾行的數據
int[][] values = new int[n][];//定義n行，但暫時每行的列數先不定義

　　2.2.2 生成二維數組，根據楊輝三角形性質，n行的數字個數為n：

for(int i = 0;i < values.length ; i++){
    values[i] = new int[i + 1];//行0有1列，行1有2列,....,行n有n+1列
}

　　2.2.3 填充二維數組：

for(int i = 0;i < values.length ; i++){
    values[i] = new int[i + 1];//行0有1列，行1有2列,....,行n有n+1列
    for(int j = 0 ; j < values[i].length ; j++){
        //根據性質1，每行的首尾都為：1
        if(j == 0 || j == value[i].lenght - 1){
            values[i][j] = 1;
        }else if(i > 1){//根據性質8，除首尾外的其它數字 = 上方數 + 上方左側的數
            values[i][j] = values[i - 1][j] + values[i - 1][j - 1];
        }
    }
}

　　2.2.4 完整代碼：

public class YangHui {
    public static void main(String[] args) {
        yangHui(8);
    }
    private static void yangHui3(int n) {
        int[][] values = new int[n][];//定義n行，但暫時每行的列數先不定義
        for(int i = 0;i < values.length ; i++){
            values[i] = new int[i + 1];//行0有1列，行1有2列,....,行n有n+1列
            for(int j = 0 ; j < values[i].length ; j++){
                //根據性質1，每行的首尾都為：1
                if(j == 0 || j == values[i].length - 1){
                    values[i][j] = 1;
                }else if(i > 1){//根據性質8，除首尾外的其它數字 = 上方數 + 上方左側的數
                    values[i][j] = values[i - 1][j] + values[i - 1][j - 1];
                }
            }
        }
        print(values);
    }
   
    private static void print(int[][] values) {
        for(int i = 0; i < values.length; i++) {
            for(int j = 0; j < values[i].length; j++) {
                System.out.printf("%-4d", values[i][j]);
            }
            System.out.println();
        }
    }
}

　　數組的方式比較好理解，但需要創建二維數組，效率較低，接下來我們看一下不需要數組的寫法。

　　三、不使用數組的方式

　　3.1 算法說明

　　 根據性質6，第n行的m個數可表示為 *C(n-1，m-1)*，即為從n-1個不同元素中取m-1個元素的組合數。

　　 我們將其表示為C(i , j)的組合數，那么就有以下算法：

1、例如：i=3、j=2的位置上，值為C(3,2)，即(3*2)/(1*2)=3/1 * 2/2 = 3
2、例如：i=5、j=3的位置上，值為C(5,3)，即(5*4*3)/(1*2*3)= 5/1 * 4/2 * 3/3 = 5 * 2 * 1 = 10
3、例如：i=7、j=4的位置上，值為C(7,4)，即(7*6*5*4)/(1*2*3*4) = 7/1 * 6/2 * 5/3 * 4/4 = 35

　　3.2 代碼實現

　　根據上述算法，我們就可以很方便的寫出以下代碼：

private static void yangHui2(int n) {
    for(int i = 0; i < n; i++) {//行
        for(int j = 0; j <= i; j++) {//列
            //計算每列的值
            int value = 1;
            for(int k = 0; k < j; k++) {
                value = value * (i-k) / (k+1);
            }
            System.out.printf("%-4d", value);
        }
        System.out.println();
    }
}