HashMap詳解

　　講解步驟

　　基礎(chǔ)知識

　　工作原理

　　關(guān)鍵代碼

　　核心方法

　　基礎(chǔ)知識

　　數(shù)組結(jié)構(gòu)

　　數(shù)組接口,在查詢數(shù)據(jù)方面,具備優(yōu)勢

　　鏈表結(jié)構(gòu)

　　鏈表結(jié)構(gòu),在增刪數(shù)據(jù)方面,具備優(yōu)勢

　　紅黑樹結(jié)構(gòu)

　　紅黑樹結(jié)構(gòu),在查詢數(shù)據(jù)方面,數(shù)據(jù)量較大的時候,具備一定的優(yōu)勢

　　什么是散列(哈希)表

　　散列表,顧名思義,就是將數(shù)據(jù)分布在不同的列

　　但是散列表并不是完全將數(shù)據(jù)分散在不同的列,而是按照某種規(guī)則,將具備同樣規(guī)則的數(shù)據(jù)存儲在同一列。

　　即具備相同規(guī)則的數(shù)據(jù)存儲在同一列,規(guī)則不同的數(shù)據(jù)分布在不同的列。

　　這種規(guī)則最終的產(chǎn)生與哈希值有關(guān)。

　　這里需要注意的事,哈希值只是確定最后存儲列的因素,也就是說不同的哈希值可能會存在同一列。

　　什么是哈希值

　　哈希值簡單的說,就是hashCode方法產(chǎn)生的值。

　　默認(rèn)的hashCode方法是由其地址值最終產(chǎn)生一個哈希值。

　　由于HashMap中的元素是否存儲是由鍵來決定,所以如果自定義的類需要存儲在鍵,且想遵循自己的存儲規(guī)則,需要重寫HashCode方法

　　又因為Map集合的鍵是不能重復(fù)的,所以需要重寫equals方法,定義去重規(guī)則。

　　工作原理

　　存儲結(jié)構(gòu)

　　HashMap基于散列法,又稱哈希法：數(shù)組+鏈表+紅黑樹。

　　HashMap需要同時存儲一對鍵和值。

　　Map集合中提供了put(key, value)方法,所有的鍵和值會被封裝到一個Entry實現(xiàn)類(Node)對象,存儲到集合中。

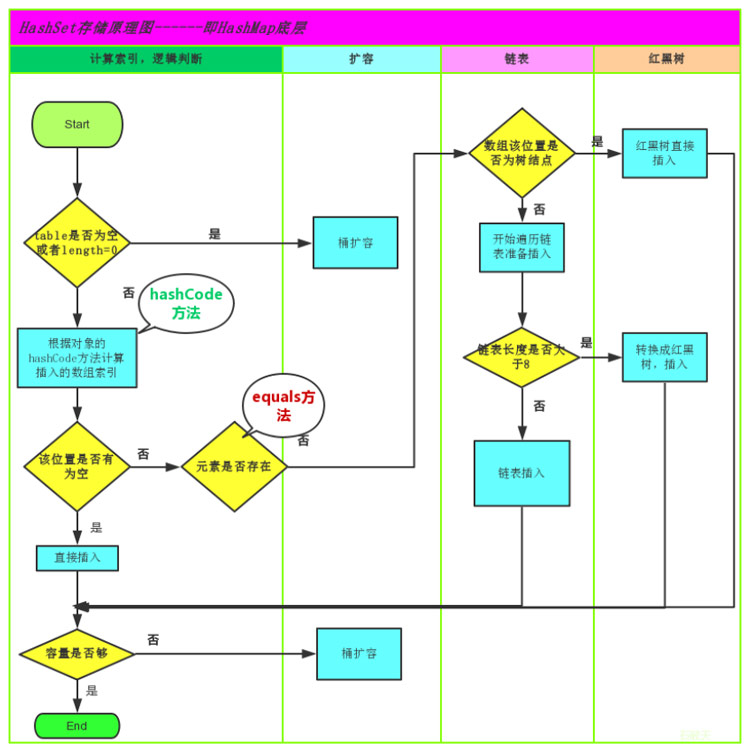
　　在存儲的過程中,會先通過hashCode()方法獲取一個哈希值,并通過這個哈希值,與數(shù)組的長度進行一定的運算,得到一個索引值(存儲的列)

　　在通過equals方法來判斷這個元素是否已存在,不存在則存儲在該列,若存儲,則保留原來的數(shù)據(jù)。

　　存儲在一列的數(shù)據(jù),將以鏈表的形式,前后關(guān)聯(lián),這樣有利于將來進行刪除的時候提高效率。

　　但是如果一列的桶結(jié)構(gòu)數(shù)據(jù)過多,就會導(dǎo)致查詢的效率降低。

　　為了優(yōu)化桶結(jié)構(gòu)帶來的問題,HashMap中會去檢查,當(dāng)一列的桶結(jié)構(gòu)數(shù)據(jù)達到8個以上,就降這一列樹化(轉(zhuǎn)變?yōu)闃浣Y(jié)構(gòu))

　　名詞理解

　　所有的數(shù)據(jù)都是以Node節(jié)點為單位。

　　hash值:哈希值,該方法內(nèi)部提供了一個擾動函數(shù)------int hashCode()

　　擾動函數(shù):用于產(chǎn)生哈希值,前16位與后16位做異或運算,提高低位隨機性。------h = key.hashCode()) ^ (h >>> 16)

　　路由尋址:由數(shù)組長度與哈希值產(chǎn)進行與操作,產(chǎn)生最終的存儲列(索引位置):(table.length-1)&node.hash

　　Hash碰撞：哈希值如果相同，就會存儲到相同的列。

　　鏈化：哈希值相同，就會存儲在同系列，產(chǎn)生桶狀結(jié)構(gòu)，桶結(jié)構(gòu)過長，查詢數(shù)據(jù)低效。

　　紅黑樹：jdk8引入,類似于二叉樹,可以避免過長的桶狀結(jié)構(gòu)

　　擴容原理

　　擴容:增加數(shù)組長度。目的在于解決數(shù)據(jù)過多，鏈化嚴(yán)重，默認(rèn)以兩倍的長度擴容。

　　①一列添加第8+個元素，且數(shù)組長度小于64，會優(yōu)先擴容。

　　②一列添加第8+個元素，且數(shù)組長度達到64個，會優(yōu)先樹化。

　　③添加元素后,若哈希表中元素總個數(shù)超過閾值(一個指定的值)，會進行擴容。

　　④擴容后，會重新根據(jù)數(shù)組長度和哈希值計算存儲位置。

　　關(guān)鍵代碼

　　核心字段

　　static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; 默認(rèn)數(shù)組大小

　　static final int MAXIMUM_CAPACITY = 1 << 30; 數(shù)組最大長度

　　static final float DEFAULT_LOAD_FACTOR = 0.75f; 默認(rèn)負(fù)載因子

　　static final int TREEIFY_THRESHOLD = 8; 樹化閾值

　　static final int UNTREEIFY_THRESHOLD = 6; 樹降級閾值

　　static final int MIN_TREEIFY_CAPACITY = 64; 樹化閾值

　　transient Node[] table; 哈希表

　　transient Set> entrySet; 鍵值對對象集合

　　transient int size; 元素長度

　　transient int modCount; 增刪元素次數(shù)

　　int threshold;擴容閾值 擴容閾值=loadFactor*capacity

　　final float loadFactor; 負(fù)載因子

　　核心方法

　　put-->putVal(存儲數(shù)據(jù))

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        //判斷表是否為空或長度為0,若滿足條件,則初始化表(體現(xiàn)了延遲加載)
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        //判斷要添加的元素對應(yīng)的列是否為空,若滿足條件,則直接插入
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
            Node<K,V> e; K k;
            //判斷元素的哈希值與要存儲列的鍵相同,則替換鍵對應(yīng)的值
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            else if (p instanceof TreeNode)
                //如果當(dāng)前節(jié)點是一個數(shù)結(jié)構(gòu)節(jié)點,按照樹結(jié)構(gòu)存儲新元素。
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {    
                for (int binCount = 0; ; ++binCount) {
                    //遍歷當(dāng)前列的節(jié)點,判斷如果當(dāng)前節(jié)點超過8個節(jié)點,則將當(dāng)前列轉(zhuǎn)為樹結(jié)構(gòu)。
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                 
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            //存在相同鍵,就值替換新值
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        //記錄操作次數(shù)
        ++modCount;
        //判斷元素個數(shù)達到指定的閾值,則進行擴容操作。
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

　　resize(擴容)

final Node<K,V>[] resize() {
        Node<K,V>[] oldTab = table;
        int oldCap = (oldTab == null) ? 0 : oldTab.length;
        int oldThr = threshold;
        int newCap, newThr = 0;
        if (oldCap > 0) {
            if (oldCap >= MAXIMUM_CAPACITY) {
                threshold = Integer.MAX_VALUE;
                return oldTab;
            }
            else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                     oldCap >= DEFAULT_INITIAL_CAPACITY)
                //修改新表的長度為舊表的兩倍
                newThr = oldThr << 1; // double threshold
        }
        else if (oldThr > 0) // initial capacity was placed in threshold
            newCap = oldThr;
        else {               // zero initial threshold signifies using defaults
            newCap = DEFAULT_INITIAL_CAPACITY;
            newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
        }
        if (newThr == 0) {
            float ft = (float)newCap * loadFactor;
            newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                      (int)ft : Integer.MAX_VALUE);
        }
        threshold = newThr;
        @SuppressWarnings({"rawtypes","unchecked"})
            Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
        table = newTab;
        //將新表內(nèi)容，重新計算位置后,放入新表
        if (oldTab != null) {
            for (int j = 0; j < oldCap; ++j) {
                Node<K,V> e;
                if ((e = oldTab[j]) != null) {
                    oldTab[j] = null;
                    if (e.next == null)
                        newTab[e.hash & (newCap - 1)] = e;
                    else if (e instanceof TreeNode)
                        ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                    else { // preserve order
                        Node<K,V> loHead = null, loTail = null;
                        Node<K,V> hiHead = null, hiTail = null;
                        Node<K,V> next;
                        do {
                            next = e.next;
                            if ((e.hash & oldCap) == 0) {
                                if (loTail == null)
                                    loHead = e;
                                else
                                    loTail.next = e;
                                loTail = e;
                            }
                            else {
                                if (hiTail == null)
                                    hiHead = e;
                                else
                                    hiTail.next = e;
                                hiTail = e;
                            }
                        } while ((e = next) != null);
                        if (loTail != null) {
                            loTail.next = null;
                            newTab[j] = loHead;
                        }
                        if (hiTail != null) {
                            hiTail.next = null;
                            newTab[j + oldCap] = hiHead;
                        }
                    }
                }
            }
        }
        return newTab;
    }

　　tableSizeFor(數(shù)組長度初始化)

二進制位運算
右移:二進制數(shù)據(jù)向右移動一位,最高位補原最高位值,原最低位舍棄。4>>1結(jié)果等于2    2>>1結(jié)果等于1  
無符號右移:二進制數(shù)據(jù)向右移動一位,最高位補0,原最低位舍棄。4>>>1結(jié)果等于2    2>>>1結(jié)果等于1    
        無符號右移動,會確保移動后一定是一個正數(shù)。
左移:二進制數(shù)據(jù)向左移動一位,最低位補0,原最高位舍棄。舉例:4<<1結(jié)果等于8   8<<1結(jié)果等于16    
或:有1則1  1001|100結(jié)果為1100(12)
   
static final int tableSizeFor(int cap) {
        //下列操作的最終目的保證了,最終的n值一定比cap大,且最接近滿足+1后數(shù)組長度定義的數(shù)值(0,3,7,15,31,63...)
        1001  100
        int n = cap - 1;  
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }